Condensation and evaporation in micro-porous membranes
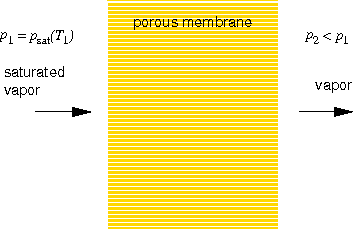
The flow of vapors through porous membranes is of interest in a number of membrane separation processes such as pervaporation and permeation. Here, the flow of saturated vapors through porous membranes is investigated. The fluid is in a state of saturated vapor upstream of the porous membrane. Downstreams, it is in a state of unsaturated vapor, see Figures 1 and 2.
|
|
|
Fig. 1: Problem statement. |
|
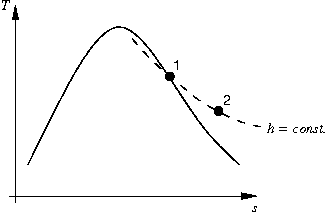
Fig. 2: Upstream state 1 and downstream state 2 of the fluid in a temperature-entropy diagram. Solid line: Dew and vapor lines. Dashed line: Isenthalpic line. |
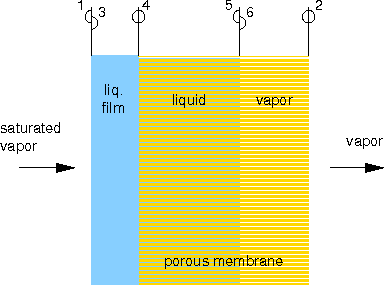
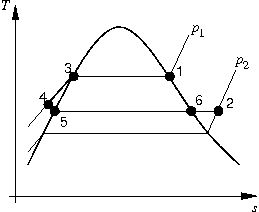
Although both states are in the vapor region, intermediate states can be in the two-phase or in the liquid region. Hence, the fluid condenses and evaporates. One possible solution to this flow problem is sketched in Figures 3 and 4. In this particular solution, the vapor condenses fully and a liquid film forms at the upstream surface of the membrane. Liquid flows through a part of the membrane and evaporates completely at a front within the membrane. Vapor flows through the remaining part of the membrane and reaches its final state 2 at the downstream surface of the membrane.
|
|
|
Fig. 3: One possible type of flow. Numbers refer to different states of the fluid, which are also shown in Fig. 4. Here, the locations are indicated where these states occur. |
|
Fig. 4: Path of the process in a temperature-entropy diagram. Thick lines: Path of the process. Thin lines: Isobaric lines. |
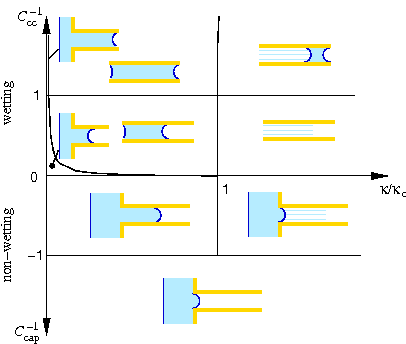
The peculiar feature of our investigation is the non-isothermal description of the flow process. Usually, flows through porous membranes are assumed to be isothermal. Here, account is taken of the temperature difference between the upstream and the downstream side of the membrane due to the Joule-Thomson effect. The flow is analyzed based on first principles: The porous membrane is modeled as a bundle of capillaries. The balances of mass, momentum and energy are applied to the fluid flow. These balances are supplemented by the Young-Laplace equation for the pressure difference caused by surface tension across a curved meniscus, by Kelvin's equation for the equilibrium vapor pressure at a curved meniscus, by Fourier's law of heat conduction and by the thermal and caloric equations of state for a real fluid. The governing equations were either solved numerically or a simplified, linearized system of governing equations was solved in closed form. For the linearized problem, nine different types of flow were found. These occur in dependence on the permeability of the membrane, on the applied pressure drop and on the contact angle between the fluid and the membrane material. The map depicted in Fig. 5 shows schematics of the different flow types and gives the conditions under which these flow types occur.
|
|
|
|
Fig. 5: Flow map. k: permeability of the membrane [m2], kc: critical permeability, Ccc = (p1 - p2)(1 - n)/(psat - pK), Ccap = ((p1 - p2)n + psat - pK)/(2σ/r), n = (dT/dp)h(dpK/dT), pK: equilbrium vapor pressure at a meniscus with radius of curvature r, σ: surface tension. The schematics for the flow types show one pore, blue stands for the liquid phase and blue striped areas symbolize a two-phase mixture. |
|
Cooperations
In February 2006, a joint research project with the group of P. Uchytil from the Prague Academy of Sciences was commenced. Uchytil's group has profound expertise on transport processes in and through porous membranes. At present, mass flow measurements are carried out. The experimental data will be compared with the theoretical predictions. The collaboration is funded by the Österreichische Austauschdienst, project nr. 09/2006. The project is partially supported by Androsch International Consulting GmbH.
Publications
T. Loimer. Linearized description of the non-isothermal flow of a saturated vapor through a micro-porous membrane, Journal of Membrane Science 301 (2007), 107 - 117.
T. Loimer. Effects of capillarity on a Joule-Thomson process of a fluid near saturation, XIVth International Symposium on Trends in Applications of Mathematics to Mechanics, Seeheim; 08-22-2004 - 08-28-2004. In: Trends in Applications of Mathematics to Mechanics, Yongqi Wang, K. Hutter (ed.), Shaker Verlag, Aachen (2005), 247 - 256.
T. Loimer. The flow of saturated vapor with positive Joule-Thomson coefficient through a porous membrane, 4th European Thermal Sciences Conference, Birmingham; 03-29-2004 - 03-31-2004. In: Proceedings of the 4th ETSC, (2004), Paper ID POM1 S14, 11 pages.
W. Schneider. Vapor flow through a porous membrane — A Throttling process with condensation and evaporation, Acta Mechanica 47 (1983), 15 - 25.