Numerical computation of lid-driven cavity flows
It is well known that symmetry breaking instabilities play a major role the understanding of the fluid physics in closed-flow systems. Therefore, we have primarily investigated the generalized driven-cavity problem for periodic boundary conditions in spanwise direction. When the Reynolds numbers associated with the wall motion is small the flow will exhibit all the symmetries of the geometry and hence it will be two-dimensional.
To study the fate of this flow when the Reynolds numbers are increased a linear stability analysis is performed. To that end the basic two-dimensional flow is computed with a finite volume or spectral method using Newton-Raphson iteration. Linearizing the Navier-Stokes equations for small perturbations of the basic flow and solving the resulting generalized eigenvalue problem numerically using the same discretization as for the basic flow, the temporal growth rates of normal modes can be determined. The locus in the parameter space where the real part of the growth rate becomes zero and the associated eigenfunction indicates the neutral stability boundary and the associated flow structure, respectively. A minimization of, e.g., the Reynolds number with respect to all neutral values then gives the critical curve or hypersurface in the paramter space. This is the lowest Reynolds number beyond which a perturbation of the basic flow grows exponentially.
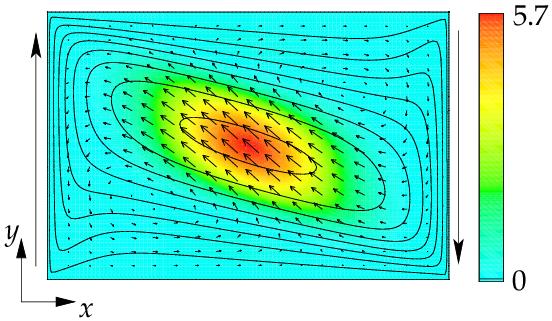
Figure 1: Basic flow streamlines (lines), energy transfer rate ... (color), and critical mode (arrows) at a coordinate z at which the energy tranfer has its maximum for aspect ratio G=1.5 and equal absolute value of the Reynolds numbers Re=192. The wall motion is indicated by the long arrows outside the figure.
Figure 1 shows a combined plot of a representative case at the critical conditions. The basic flow streamlines are indicated by lines. The color is coding a the most important contribution to the rate of energy transfer from the basic flow (lines) to the unstable mode (arrows) which is shown in a cut at a z-level at which the energy transfer rate takes its maximum. The most important region for the energy transfer is the center of the basic vortex whose central streamlines are elliptic. One can argue that the instability is due to the elliptic instability process, a generic mechanism by which strained vortices become unstable. The nonlinear evolution beyond the critical Reynolds numbers can be investigated by a full simulation of the Navier-Stokes equations. For the elliptic instability we have found that the supercritical flow patterns are quite robust and exist as steady flows in a wide range of Reynolds number (see fig. 4 in the experimental section).

Figure 2: Critical hypersurface of the two-dimensional generalized lid-driven cavity flow (color). The grey objects indicate regions in which the basic two.dimensional flow is not unique.
The parameters space is made up of the the Reynolds numbers and the aspect ratio G of the cavity. Figure 2 shows the critical hypersurface for the instability of the two-dimensional flow (color). It is the envelope of the innermost neutral hypersurfaces und thus made up of different facettes which each belongs to a qualitiatively different critical mode. We found more than 20 different critical modes. Only the most important ones are shown in the figure. Among these are the elliptic instability (blue), the cooperative instability (red), the centrifugal instability (green), and the quadripolar instability (green). Note that the two latter instabilities merge smoothly into each other when the Reynolds numbers are varied. The situation is complicated to some degree by the existence of multiple two-dimensional basic flows (shown in grey). The region in the lower right does not overlap with the stability balloon. However, the upper left region of nonuniquness collides with the stability ballon and all possible basic states in the overlap region need to be investigated individually.
A further introduction is provided in H. C. Kuhlmann and S. Albensoeder, Strained vortices in driven cavities, Z. Angew. Math. Mech. 85, 387-399 (2005).
